Zeno von Elea ist ein griechischer Logiker und Philosoph, der hauptsächlich für die ihm zu Ehren genannten Paradoxien bekannt ist. Über sein Leben ist nicht viel bekannt. Die Heimatstadt von Zeno ist Elea. Auch in den Schriften Platons wurde das Treffen des Philosophen mit Sokrates erwähnt.
Um 465 v e. Zeno schrieb ein Buch, in dem er alle seine Ideen skizzierte. Aber leider hat es unsere Tage nicht erreicht. Der Legende nach starb der Philosoph in einem Kampf mit einem Tyrannen (vermutlich dem Oberhaupt von Elea Nearch). Alle Informationen über Elea wurden Stück für Stück gesammelt: aus den Werken von Platon (geb. 60 Jahre später Zeno), Aristoteles und Diogenes Laertius, die drei Jahrhunderte später ein Buch mit Biografien griechischer Philosophen schrieben. Zeno wird auch in den Schriften der späteren Vertreter der Schule der griechischen Philosophie erwähnt: Themistik (4. Jahrhundert v. Chr.), Alexander Afrodinsky (3. Jahrhundert v. Chr.) Sowie Philoponus und Simplicius (beide lebten im 6. Jahrhundert v. Chr.).. Darüber hinaus stimmen die Daten in diesen Quellen so gut überein, dass alle Ideen des Philosophen daraus rekonstruiert werden können. In diesem Artikel werden wir Ihnen die Paradoxien von Zeno erläutern. Also fangen wir an.

Paradoxe des Sets
Seit der Ära von Pythagoras wurden Raum und Zeit ausschließlich aus mathematischer Sicht betrachtet. Das heißt, es wurde angenommen, dass sie aus vielen Punkten und Punkten bestehen. Sie haben jedoch eine Eigenschaft, die leichter zu erfassen als zu definieren ist, nämlich „Kontinuität“. Einige Zeno-Paradoxe beweisen, dass es nicht in Momente oder Punkte unterteilt werden kann. Die Argumentation des Philosophen läuft auf Folgendes hinaus: „Nehmen wir an, wir haben die Teilung bis zum Ende abgeschlossen. Dann ist nur eine der beiden Optionen wahr: Entweder erhalten wir die minimal möglichen Mengen oder Teile, die unteilbar, aber unendlich groß sind, oder die Teilung führt uns zu Teilen ohne Größe, da die Kontinuität, die homogen ist, unter keinen Umständen teilbar sein muss. Es kann nicht in einem Teil teilbar sein, aber nicht in dem anderen. Leider sind beide Ergebnisse ziemlich lächerlich. Der erste Grund ist die Tatsache, dass der Teilungsprozess nicht beendet werden kann, während der Rest Teile enthält, die einen Wert haben. Und der zweite Grund ist, dass in einer solchen Situation zunächst das Ganze aus dem Nichts entstanden wäre. “ Simplicius schrieb dieses Argument Parmenides zu, aber es ist wahrscheinlicher, dass sein Autor Zeno ist. Wir gehen weiter.
Zenos Paradoxe der Bewegung
Sie werden in den meisten Büchern, die dem Philosophen gewidmet sind, berücksichtigt, weil sie mit Beweisen für die Gefühle der Eleatiker in Dissonanz geraten. In Bezug auf die Bewegung werden die folgenden Zeno-Paradoxe unterschieden: "Pfeil", "Dichotomie", "Achilles" und "Stufen". Und sie kamen dank Aristoteles zu uns. Schauen wir sie uns genauer an.
Pfeil
Ein anderer Name ist das Zeno-Quantenparadoxon. Der Philosoph behauptet, dass alles entweder stillsteht oder sich bewegt. Aber nichts ist in Bewegung, wenn der belegte Raum gleich lang ist. Zu einem bestimmten Zeitpunkt befindet sich der bewegliche Pfeil an einer Stelle. Daher bewegt es sich nicht. Simplicius formulierte dieses Paradoxon in Kurzform: „Ein Flugobjekt nimmt im Raum einen gleichen Platz ein, aber das, was im Raum den gleichen Platz einnimmt, bewegt sich nicht. Deshalb ist der Pfeil in Ruhe. “ Femistius und Phelopon formulierten ähnliche Optionen.
"Dichotomie"
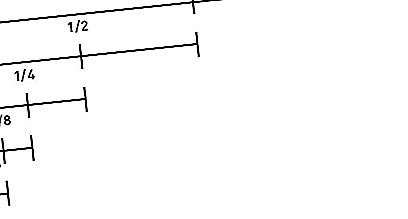
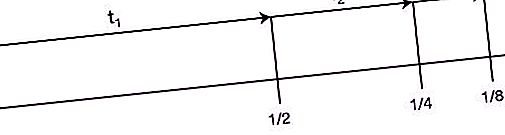
Platz zwei in der Liste der "Zeno Paradoxes". Es lautet wie folgt: „Bevor ein Objekt, das sich zu bewegen beginnt, eine bestimmte Strecke zurücklegen kann, muss es die Hälfte dieses Pfades, dann die Hälfte der verbleibenden usw. bis ins Unendliche überwinden. Da bei wiederholten Teilungen der Entfernung in zwei Hälften das Segment ständig endlich wird und die Anzahl dieser Segmente unendlich ist, kann diese Entfernung nicht in einer endlichen Zeit überwunden werden. Darüber hinaus gilt dieses Argument sowohl für kleine Entfernungen als auch für hohe Geschwindigkeiten. Daher ist jede Bewegung unmöglich. Das heißt, der Läufer kann nicht einmal starten."
Dieses Paradoxon hat Simplicius ausführlich kommentiert und darauf hingewiesen, dass in diesem Fall unendlich viele Berührungen in einer endlichen Zeit vorgenommen werden müssen. "Jeder, der etwas berührt, kann zählen, aber die unendliche Menge kann nicht aussortiert oder gezählt werden." Oder, wie Philopon es ausdrückte, eine unendliche Menge ist undefinierbar.
Achilles
Auch als Paradox der Zeno-Schildkröte bekannt. Dies ist das beliebteste philosophische Argument. In diesem Paradox der Bewegung tritt Achilles in einem Lauf mit einer Schildkröte an, die zu Beginn ein kleines Handicap erhält. Das Paradoxe ist, dass die griechische Kriegerin die Schildkröte nicht einholen kann, da sie zuerst den Ort ihres Starts erreicht und sie bereits am nächsten Punkt sein wird. Das heißt, die Schildkröte wird immer vor Achilles sein.
Dieses Paradoxon ist einer Dichotomie sehr ähnlich, aber hier verläuft die unendliche Teilung nach dem Fortschritt. Im Falle einer Dichotomie gab es eine Regression. Zum Beispiel kann derselbe Läufer nicht starten, weil er seinen Standort nicht verlassen kann. Und in der Situation mit Achilles wird der Läufer, selbst wenn er sich in Bewegung setzt, nirgendwohin rennen.
"Bühne"
Wenn wir alle Paradoxe von Zeno in Bezug auf die Komplexität vergleichen, wäre dies der Gewinner. Es ist schwieriger als andere zu erklären. Simplicius und Aristoteles haben diese Argumentation fragmentarisch beschrieben, und man kann sich nicht mit 100% iger Sicherheit auf ihre Zuverlässigkeit verlassen. Die Rekonstruktion dieses Paradoxons hat die folgende Form: A1, A2, A3 und A4 sind bewegungslose Körper gleicher Größe, und B1, B2, B3 und B4 sind Körper der gleichen Größe wie A. B-Körper bewegen sich nach rechts, so dass jedes B passiert Und das in einem Augenblick, dem kleinsten möglichen Zeitraum. Sei B1, B2, B3 und B4 Körper, die mit A und B identisch sind, und bewege dich relativ zu A nach links, wobei jeder der Körper in einem Augenblick überwunden wird.
Offensichtlich hat B1 alle vier Körper von B überwunden. Nehmen wir für eine Einheit die Zeit, die ein Körper von B benötigt, um einen Körper von B zu durchlaufen. In diesem Fall wurden vier Einheiten für alle Bewegungen benötigt. Es wurde jedoch angenommen, dass die beiden Momente, die für diese Bewegung vergingen, minimal und daher unteilbar waren. Daraus folgt, dass vier unteilbare Einheiten zwei unteilbaren Einheiten entsprechen.